What Is A Sinusoidal Function

The sinusoidal functions (sine and cosine) appear everywhere, and they play an of import office in circuit assay. The sinusoidal functions provide a expert approximation for describing a circuit'south input and output beliefs not just in electrical applied science but in many branches of scientific discipline and engineering.

The sinusoidal role is periodic, meaning its graph contains a bones shape that repeats over and over indefinitely. The function goes on forever, oscillating through countless peaks and valleys in both negative and positive directions of fourth dimension. Here are some key parts of the office:

The aamplitude V _A defines the maximum and minimum peaks of the oscillations.
Frequency f ₀ describes the number of oscillations in ane second.
The menstruation T ₀ defines the fourth dimension required to consummate 1 cycle.

The menses and frequency are reciprocals of each other, governed past the following mathematical relationship:

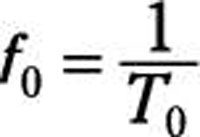
Hither is a cosine function you tin use as the reference signal:

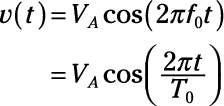
Y'all tin move sinusoidal functions left or right with a time shift as well as increase or decrease the amplitude. You can also describe a sinusoidal function with a phase shift in terms of a linear combination of sine and cosine functions. Here is a cosine function and a shifted cosine function with a phase shift of π/2.

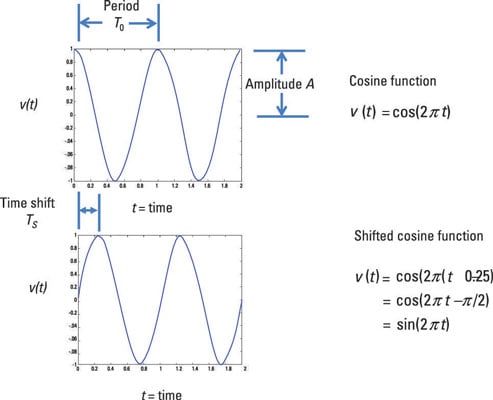
Phase shifts in a sinusoidal function

A betoken that's out of phase has been shifted left or correct when compared to a reference point:

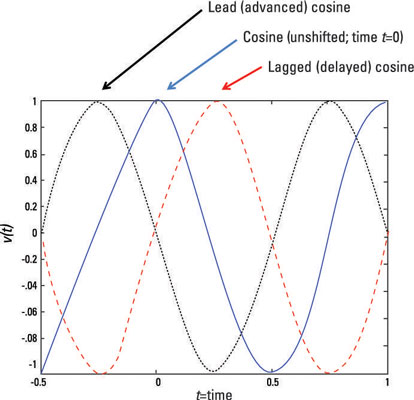
Right shift: When a role moves right, then the function is said to be delayed. The delayed cosine has its peak occur after the origin. A delayed signal is also said to be a lag bespeak considering the signal arrives later than expected.
Left shift: When the cosine function is shifted left, the shifted office is said to be avant-garde. The acme of the advanced signal occurs just earlier the origin. An advanced bespeak is besides chosen a pb signal because the lead signal arrives earlier than expected.

Here are examples of unshifted, lagged, and lead cosine functions.

To encounter what a phase shift looks like mathematically, first have a wait at the reference bespeak:

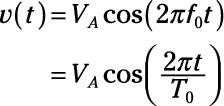
At t = 0, the positive top V _A serves as a reference point. To motion the reference point past fourth dimension shift T _S , replace the t with (t – T _South ):

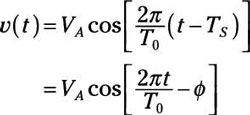
where

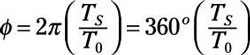
The factor ϕ is the stage shift (or angle). The phase shift is the angle betwixt t = 0 and the nearest positive peak. Y'all tin can view the preceding equation as the polar representation of the sinusoid. When the stage shift is π/2, and then the shifted cosine is a sine office.

Express the phase bending in radians to make sure it's in the same units as the statement of the cosine (2πt/T ₀ – ϕ). Angles tin can exist expressed in either radians or degrees; brand certain you lot use the right setting on your computer.

When you take a phase shift ϕ at the output when compared to the input, information technology's unremarkably acquired by the excursion itself.

Expand a sinusoidal function and observe Fourier coefficients

The general sinusoid v(t) involves the cosine of a deviation of angles. In many applications, you can expand the general sinusoid using the following trigonometric identity:

Expanding the full general sinusoid v(t) leads to

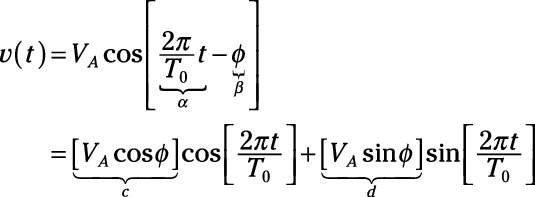
The terms c and d are simply special constants called Fourier coefficients. You can express the waveform as a combination of sines and cosines every bit follows:

The function v(t) describes a sinusoidal indicate in rectangular form.

If you lot know your complex numbers going between polar and rectangular forms, then you tin go between the two forms of the sinusoids. The Fourier coefficients c and d are related by the amplitude V _A and phase ϕ:

If you go back to detect V _A and ϕ from the Fourier coefficients c and d, you current of air up with these expressions:

The inverse tangent function on a calculator has a positive or negative 180° (or π) phase ambiguity. You tin can figure out the phase by looking at the signs of the Fourier coefficients c and d. Describe the points c and d on the rectangular system, where c is the x-component (or abscissa) and d is the y-component (or ordinate).

The ratio of d/c can exist negative in Quadrants II and IV. Using the rectangular arrangement helps you make up one's mind the angles when taking the arctangent, whose range is from –π/2 to π/2.

Connect sinusoidal functions to exponentials with Euler's formula

Euler'south formula connects trig functions with complex exponential functions. The formula states that for any real number θ, you have the following complex exponential expressions:

The exponent j θ is an imaginary number, where j = √-1.

The imaginary number j is the aforementioned as the number i from your math classes, but all the cool people use j for imaginary numbers considering i stands for current.

You tin can add and subtract the two preceding equations to go the post-obit relationships:

These equations say that the cosine and sine functions are built as a combination of complex exponentials. The circuitous exponentials play an important role when you're analyzing complex circuits that accept storage devices such equally capacitors and inductors.